|
Spreading Resistance of Circular Sources on
Compound and Isotropic Disks
|
Summary
This application calculates thermal spreading resistance
for a circular source on a
circular disk, semi-infinite circular cylinder,
or half-space.
Solutions are available for a compound medium with
two layers having different thicknesses
and thermal conductivities,
and an isotropic medium with constant properties throughout.
For the finite disk cases, two boundary conditions
for the lower surface are considered:
a
uniform film coefficient, corresponding to convective or
contact cooling,
and a uniform
temperature boundary condition.
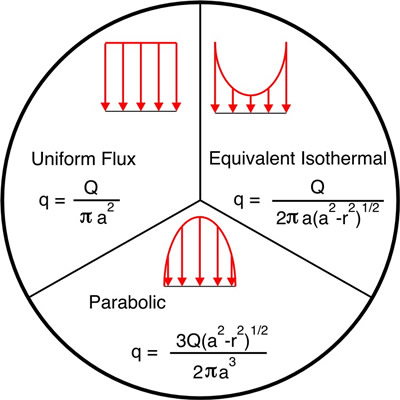
The heat flux over the circular source is either uniform, parabolic, or
distributed such that the resulting source is equivalent to an isothermal
boundary condition.
Background
Thermal spreading resistance occurs whenever heat leaves a source of finite
dimensions and enters a larger region. The particular case modeled by this
calculator involves a planar circular heat source of radius a in
perfect contact with the top surface of a
circular disk or semi-infinite circular cylinder of radius b.
For the finite disk, the overall thickness of the disk is t, and the
disk is cooled over its entire bottom surface either with a uniform
convective or contact conductance h, or an isothermal boundary.
The lateral and non-source top surface boundaries of the disk or cylinder
are adiabatic.
The total system thermal resistance Rtotal
is defined by:
Rtotal = ( Tsource - Tsink ) / Q
where: |
Tsource = |
area-mean source temperature
( oC) |
|
Tsink = |
mean heat sink temperature ( oC)
|
| Q = |
heat flow rate through the heat flux channel
(W) |
Rtotal = Rs + R1D
where Rs is the thermal spreading resistance of the
system and R1D is the one-dimesional thermal resistance,
defined as:
R1D =
( t1 / k1 +
t2 /
k2 +
1 / h ) /
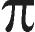b2
For the general case of a rectangular source area on a finite, two-layer
rectangular heat flux channel, the spreading resistance will depend on
several geometric and the heat flux distribution:
Rs = f ( a, b,
t1, t2,
k1, k2,
h
)
Three flux distributions are included in this applications:
The results for total, one-dimensional, and spreading resistance are
presented in both dimensional and dimensionless forms, where the resistance
is non-dimensionalized by:
R* = 4 k1 a R
All calculations are based on methods described in
M.M. Yovanovich, J.R. Culham and P. Teertstra,
"Modeling Thermal Resistance of Diamond Spreader on Copper Heat Sink
Systems," presented at the IEPS Electronics Packaging Conference,
Sept. 29 - Oct. 1, Austin, TX, 1996, and
M.M. Yovanovich, C.H. Tien and G.E. Schneider, "General Solution of
Constriction Resistance Within a Compound Disk,"
Heat Transfer, Thermal Control and Heat Pipes, AIAA Progress in
Astronautics and Aeronautics, Vol. 70, 1980
Instructions
- Click on the image below that best describes your problem
- When the required tables are loaded, enter
all input values in the table on the left
- Browser will calculate when the Calculate button is clicked
- Depending on the speed of your machine and
the number of terms, the solution may take
a while to compute
Copyright © 2006 Microelectronics Heat Transfer Laboratory
